快捷导航
上海总部:上海市 普陀区 怒江北路598号 红星世贸大厦B栋1206室
邮编:200333
总机:021-61243616
传真:021-61243616*819
业务邮箱:
sales@hmelectronics.com.cn
邮编:200333
总机:021-61243616
传真:021-61243616*819
业务邮箱:
sales@hmelectronics.com.cn
资讯文章
优化脉宽调制(PWM)简述和单相半桥逆变器、消除谐波一般方法
优化脉宽调制(PWM)简述和单相半桥逆变器、消除谐波一般方法
PWM技术能消除和削弱高次谐波,其中脉冲的个数、宽度以及分布和消除谐波都有其规律性,掌握其规律就可以根据要改进的目标,倒如:电压波形畸变率小.驱动异步电动机脉动转矩小,电动机损耗小,提高效率等要求去优化PWM。因为低次谐波对性能影响大,因此优化PWM着重于消除低次谐波,更高次数谐波可通过滤波电路解决。例如5次、7次谐波对产生脉动转矩起主要作用,因此为減小脉动转矩,优化PWM首先集中要消除5次、7次谐波。
单相半桥逆变器,消除谐波一般方法
图7-21为一单相半桥逆变器。图中VTh1导通,VTh2关断,a点电位为正,VTh1关断VTh2导通,a点电位为负。
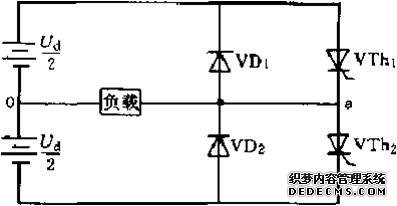 图7-21单相半桥逆变器
图7-21单相半桥逆变器 图7-22为单相半桥逆变器输出的一般波形。一个周期的波形具有半波对称性和单位幅值,每半个周期有M次斩波,斩波由a1,a2,a3,....a2M确定。波形可用付氏级数表示
其中
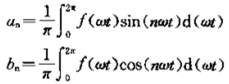
将f(ωt)代入an、bn,利用半波对称性
得
其中 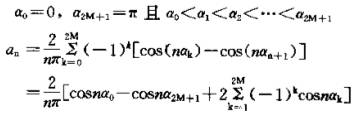
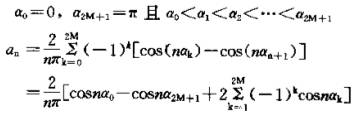
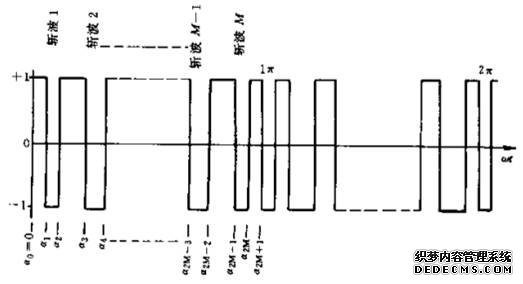
图7-22半桥逆变器产生的一般波形
因
α0=0,α2M+1=π
所以 cosnα0=1 ,cosnα2M+1 = ( -1)π
同理
根据波形的半波对称性
n为偶数时 an=0, bn = 0
n为奇数时

解上述方程,因为是2M个变量α1α2α3...α2m的函数,含M个谐波为零,可得到2M个方程.
如果是个具有四分之一周期对称性质的波形的话,会使问题更简单。
f(ωt)=f(π-ωt)
αk=π-α(2m-k+1) k=1,2,3...,m
sinnαk=sinn(π-α2m-k+1)
=[sinnπcosnα(2m-k+1) -cosnπsinnα(2m-k+1)]
当n为奇数时:sinnπ=0 ,cosnπ=-1
因 sinnαk=sinnα2m-k+1
所以
而 cosnαk=cosn[π-α(2m-k+1) ]
当n为奇数时 cosnαk=-cosnα2m-k+1
所以
例如:直流环节电压为Ud波形单位帽值相当Ud/2,M = 4,保留基波幅度为给定值,消除5次、7次、11次谐波则
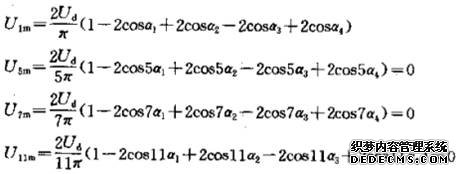
可解出 a1 、a2 、a3、a4。
结论:波形在每半周期内有M个斩波,并且有四分之一周期对称性,则可以消除任意M个谐波.
(文/上海合美电子科技有限公司)
上海合美电子科技有限公司
电话:021-61243616 传真:021-61243616*819 地址:上海市 普陀区 怒江北路598号 红星世贸大厦B栋1206室
沪ICP备16054338号-2


沪公网安备 31010702002036号